이동평균선 (Moving Average Line)
이동평균선 개요
- 이동평균은 기술적 분석, 특히 기술적 지표 분석의 기초를 이룬다. 이동평균기법이 최초로 주식시장에 소개된 이후로 이동평균을 이용한 분석기법은 다양하게 개발됐다.
- 가장 널리 알려진 기법은 ‘현재 가격과 이동평균선을 비교’하고 ‘이동평균선의 기울기 변화를 추적’하거나, ‘이동평균선간의 교차와 배열’ 등을 이용하여 시장 참여자들의 생각이 어떻게 변하고 있는 지에 대한 정보를 알아내는 것 등이다.
- 이동평균은 단기적인 변동(fluctuations)을 완만하게 하여 상대적인 긴 기간 동안의 추세나 사이클 등을 더욱 분명하게 나타낸다는 장점 때문에 ‘움직이는 추세선(moving trend line)’이 라고 불리며 활용되기도 한다.
- 다만 이동평균은 ‘후행성’이라는 결정적 단점을 내포하고 있다. 그러나 이 단점을 역이용하면 투자판단에 좋은 정보를 얻을 수 있다.
- 이동평균은 주로 가격을 분석하는데 이용하지만, 다양한 시계열의 분석 예를 들면 거래량 또는 거래대금 등의 분석에도 이용된다. 또한 다양한 기술적 지표를 개발하는 데 기초가 되기도 한다.
- 이동평균은 크게 ① 단순 이동평균(Simple moving average), ② 가중 이동평균(Weightedmoving average), ③ 지수 이동평균(Exponential moving average) 등으로 나뉜다.
이동평균의 종류
단순 이동평균(Simple Moving Average)
계산식
단순 이동평균 기법은 계산 방식이 쉽기 때문에 가장 널리 이용되는 방법 중 하나이다. 다음은 t 시점에 n일 단순 이동평균을 구하는 식이다.

한편 위 식 1을 이용하여 t-1 시점의 n일 단순 이동평균을 구한다면 다음과 같다.
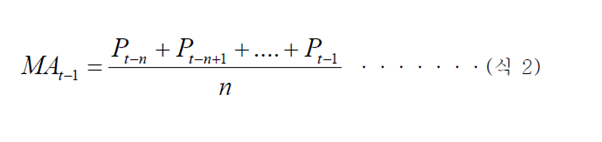
이상과 같은 과정을 통해 최초에 이동 평균값을 구할 때는 식 1또는 2의 절차를 거쳐야 하지만,
두번째부터 이동평균을 구할 때부터는 식 3을 이용하여 간단하게 이동평균을 구할 수 있다는 것
을 알 수 있다. 식 3의 결과를 표 1의 간단한 예시를 통해 보면 이해에 도움이 된다.
표1)
일자 가격 5일이동평균계산 5일 이동평균값

단순 이동평균 기법의 문제점
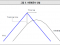
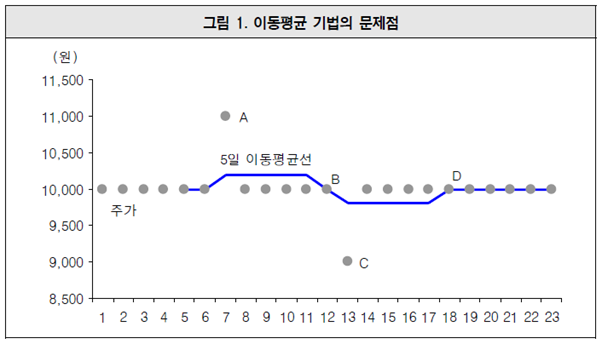
그런데 단순 이동평균 방식은 결정적 문제점을 내포하고 있다. 가장 중요한 문제점은 현재 시장 데이터는 과소, 과거 데이터는 과대하게 반영돼 있다는 것이다. 예를 들어 다음과 그림 1과 같은 가격 흐름이 있다고 가정하자.
전혀 움직임이 없던 가격은 A시점에 11,000원으로 10%나 급등한다. 이 때 5일 이동평균선도 즉각적으로 반응하고 있는 것을 볼 수 있다. 그런데 B시점에서는 전혀 가격이 변화가 없었음에도 불구하고 이동평균선이 하락하는 것으로 나타난다.
이는 6일 전인 A시점에서 급등했던 가격 데이터가 빠져나가기 때문이다. 즉 현재 가격의 변화 없이 계산 방식의 단점으로 인하여 이동평균선이 필요 없이 반응한 것이다.
한편 C시점에서 가격은 9,000원으로 10% 급락하였다. A시점과 마찬가지로 C시점에서 이동평균선은 가격의 하락을 제대로 반영하였다. 그러나 역시 이후 아무런 가격 변동이 없었음에도 불구하고 D시점에서 이동평균선은 전일 대비 상승하는 결과를 나타냈다.
이는 6일전 급락했던 가격인 9,000원이 5일 이동평균값 계산에서 빠져나갔기 때문이다.
이와 같은 문제점을 개선하기 위하여 사용되는 방식이 지수 이동평균(Exponential MovingAverage; EMA)과 가중 이동평균(Weighted Moving Average: WMA)이다.
가중 이동평균(Weighted Moving Average)
이해
지수 이동평균에 대해 알아보기에 앞서, 가중 이동평균(Weighted Moving Average)에 대하여 먼저 이해할 필요가 있다. 명칭에서 알 수 있듯이 가중 이동평균은 이동평균을 계산하는데 있어 시점별로 다른 가중치를 부여함으로서 단순 이동평균기법을 보완할 수 있는 계산법이다.
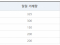
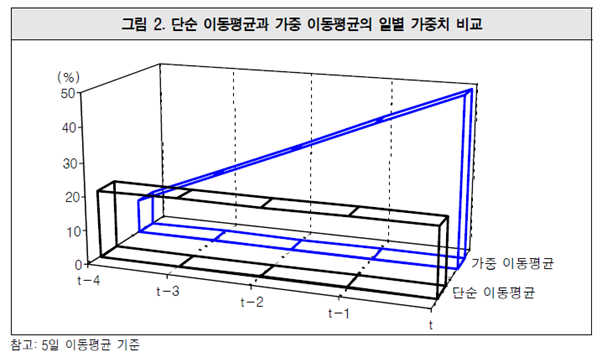
5일 이동평균을 중심으로 가중치를 비교한다면 다음 그림 2와 같이 간단하게 표현된다. 즉 단순 이동평균은 현재 시점부터 4일전 시점까지 가격에 각각 20%의 동등한 가중치가 부여된다고 한다면,가중 이동평균은 가장 최근에는 50% 그리고 전일에는 40%의 식으로 가중치가 부여돼 4일전에는 10%의 가장 작은 가중치를 부여하는 식이다. 이와 같이 함으로써 가장 최근 가격의 변화에 민감하에 반응할 수 있도록 하고 과거 가격의 영향은 제한적으로만 반영될 수 있는 것이다.
계산식
가중 이동평균을 구하는 산식은 아래와 같다.
이 식에서 가중치(w)를 부여하는 방식은 일정수치 증가법, 비율법이 있다. 일정수치 증가법은 가중치가 선형(5, 4, 3, 2, 1의 방식)으로 감소하도록하는 방법이고, 비율법은 정률(0.6의 비율일 경우 5, 3, 1.8, 1.08, 0.864의 방식)으로 가중치가
감소하도록 하는 방법이다.

지수 이동평균(Exponential Moving Average; EMA)
이해
지수 이동평균은 가중 이동평균의 한 종류라고 볼 수 있다. 기간별로 가중치를 달리 적용하는 것 이 같기 때문이다. 다만 가중 이동평균과 달리 가중치 대신 0보다 크고 1보다 작은 지수(exponential factor)를 이용한다는 것이 다르다.
지수를 k라고 한다면, k는 0<k<1 이므로 가장최근 가격에는 지수에 0승을 한 값을 곱하고 그 이후에는 지수에 (n-1)승을 곱하는 식으로 지수 이동평균이 구해지게 된다. 다음은 지수 이동평균의 산식이다.
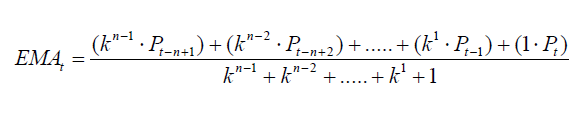
그런데 다소 복잡한 위 식 5를 단순화하기 위하여 다음과 같이 단순화를 시도하겠다.
가장 먼저 식에 변화를 주기 위하여 t-1 시점의 지수 이동평균에 k를 곱하여 빼주면 다음과 같은 식 6이
된다.
한편 위 식 6의 우측 변의 분자와 분모에 모두 (1-k)를 곱하면 다음과 같은 식 7이 된다.
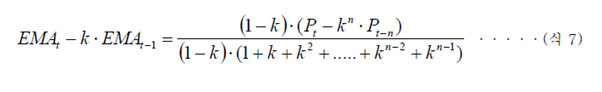
그런데 만약 이 식에서 n이 무한대로 커진다고 가정할 경우 분자의k n 값이 0에 수렴하게 되고
따라서 t n k n P− ⋅ 의 값도 0이 되어 분자는 t P 만이 남게 되며 분모는 1만 남게 되어 최종적으로
다음 과 같은 식 8과 같이 된다.
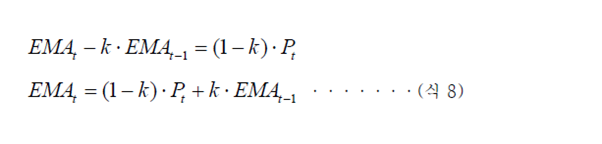
위 식에서 k를 0.5라고 가정하면 t일의 지수 이동평균 즉 t EMA 는 t일의 가격에 50%의 가중치를 부여하고 t-1일의 지수 이동평균 t −1 EMA 에 나머지 50%의 가중치를 부여하여 계산된다는 것을 알 수 있다.
한편 위 식 8을 한번 더 간단히 하기 위하여 (1-k)를 c라고 하면 다음 식 9와 같이 정리된다.
Richard D Donchian과 함께 이동평균을 이용한 투자기법 개발에 기여한 Jack K Hutson에 의하면 위 식 9에서 c 값의 최적치는 2 (n +1) 이라고 하였다. 이를 적용하여 (1− k ) = c 라는 식에 대입하면 k 값의 최적치는 (n −1) (n +1)로도 표현이 가능하다.
식 9를 이용하여 5일 지수 이동평균선을 구하는 예를 다음과 같이 제시할 수 있다. 우선 c 값을 정한다면 c = 2 (n +1) = 2 (5 +1) = 0.3333... 이 된다. 이를 앞서 표 1의 예에 적용하도록 해보자. 그렇다면 다음 표 2와 같다.
표2)
일자 가격 5일 이동평균계산 5일 이동평균 값





 이동평균선 - 2편 실전적용(매매기법)
이동평균선 - 2편 실전적용(매매기법)
 이동평균선 Guru의 조언
이동평균선 Guru의 조언